Building a Black-Scholes Calculator: Learning by Doing
I wanted to understand the Black-Scholes model — not just memorize the formula, but really get it. So instead of reading ten tutorials, I decided to build a calculator from scratch using Python and AI support.
What is Black-Scholes and Why It Matters
The Black-Scholes model is a mathematical formula used to price European-style options. Developed in 1973 by Fischer Black and Myron Scholes (with Robert Merton's contributions), it revolutionized options trading by providing a theoretical framework for pricing options. The model's impact was so significant that Scholes and Merton received the Nobel Prize in Economics in 1997.
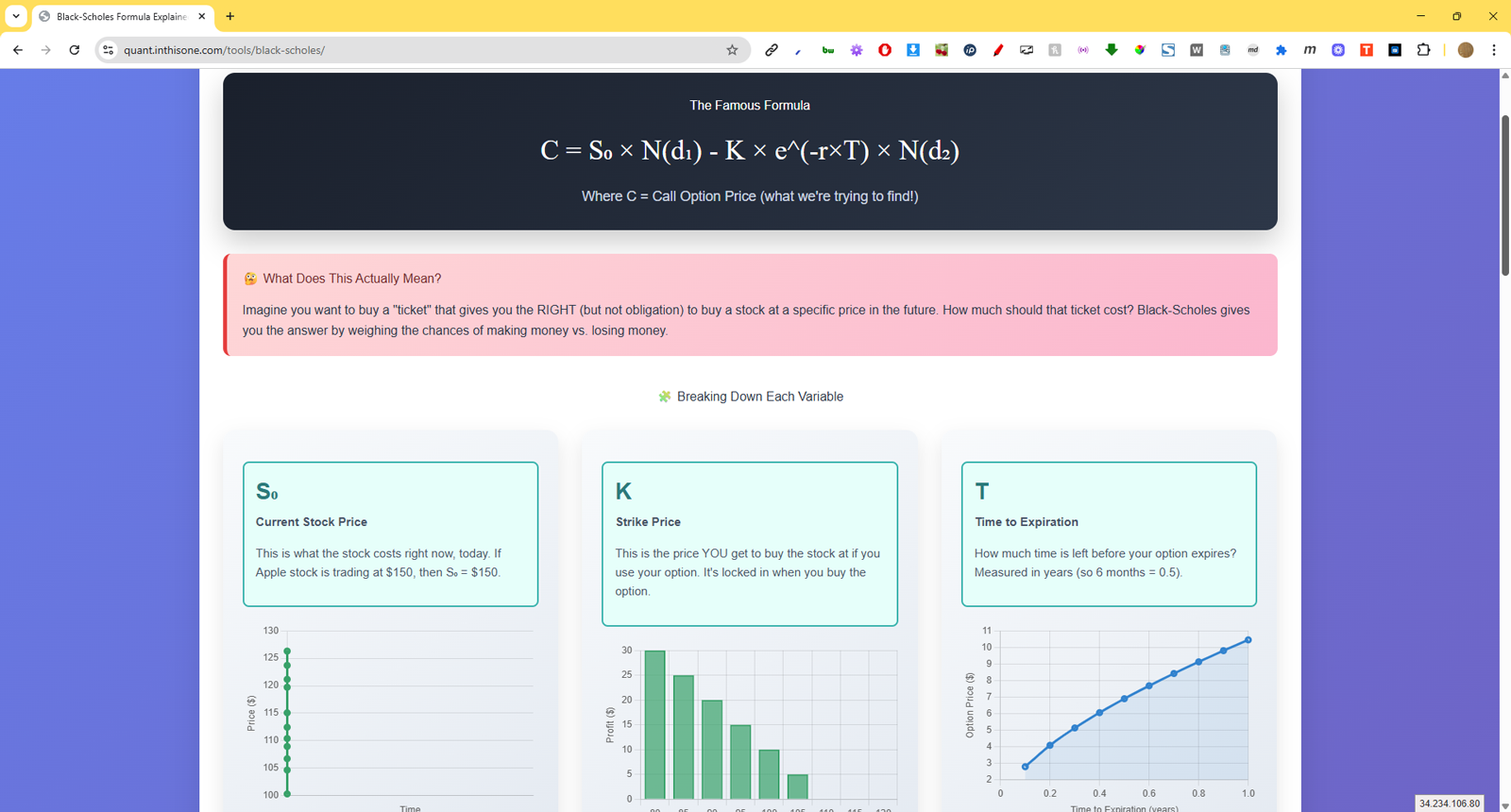
The formula looks intimidating at first:
$$ C = S N(d_1) - K e^{-rT} N(d_2) $$
$$ P = K e^{-rT} N(-d_2) - S N(-d_1) $$
Where:
$$ d_1 = \frac{\ln(S/K) + (r + \sigma^2 / 2)T}{\sigma \sqrt{T}}, \quad d_2 = d_1 - \sigma \sqrt{T} $$
But each component has a clear meaning:
- S: Current stock price
- K: Strike price
- T: Time to expiration
- r: Risk-free interest rate
- σ: Volatility
- N(): Cumulative normal distribution
Why I Built This
My motivation came from three main sources:
- Curiosity: I wanted to understand how options pricing actually works, not just read about it
- Hands-on Learning: Building something forces you to understand the details
- AI Partnership: I used AI to help generate the initial code, then iteratively refined it
The process of building the calculator taught me more than any textbook could. I had to:
- Implement the mathematical formulas correctly
- Create an intuitive user interface
- Add real-time updates and visualizations
- Handle edge cases and error conditions
The Development Process
I started with a basic Python implementation of the Black-Scholes formula, then added:
- Interactive sliders for all parameters
- Real-time price updates
- Visual charts showing the impact of each parameter
- Detailed explanations of the underlying mathematics
The most interesting part was seeing how each parameter affects the option price:
- Higher volatility increases both call and put prices
- Longer time to expiration increases option values
- Higher interest rates increase call prices but decrease put prices
Learning Outcomes
Building this calculator taught me several valuable lessons:
- Understanding vs. Memorization: Building something forces you to understand the underlying concepts
- AI as a Learning Tool: AI can help generate initial code, but you need to understand it to improve it
- Visual Learning: Interactive visualizations make complex concepts more intuitive
- Practical Application: Real-world implementation reveals nuances that theory alone doesn't show
Try It Yourself
You can try the calculator at quant.inthisone.com/tools/black-scholes or view the source code on GitHub.
Next Steps
This project has sparked my interest in other quantitative finance topics. I'm planning to explore:
- More complex options pricing models
- Greeks and risk management
- Portfolio optimization
- Machine learning applications in finance
Remember, the best way to learn is by doing. Don't just read about quantitative finance — build something!